Chapter 2 - My Risk Book

Compound Interest Rate

Posted on 20222022 by M. Humayun Kabir

Compound Interest Rates

Let's re-state our previous example: if $1,000 is invested for a year at the interest rate of 10% per annum with annual compounding, you are going to receive at the end of the year a return of

$\$1,000 \times 0.10 = \$100$

Your investment earns $100 at the end of the year. The value of your investment at the end of the first year is $1,100. We can write the value of your investment as

$\$1,000 + \$1,000 \times 0.10 = \$1,000(1+0.10) = \$1,100$

If $1,000 is invested for two years at the interest rate of 10% per annum with annual compounding, you are going to receive at the end of the first year a return of

$\$1,000 \times 0.10 = \$100$

The value of your investment is

$\$1,000 + \$1,000 \times 0.10 = \$1,100$

$\$1,000(1+0.10) = \$1,100$

In the second year, you invest $1,100 at 10% for another year. The value of your investment would be

$\$1,100 + \$1,100 \times 0.10 = \$1,210$

$\$1,100(1+0.10) = \$1,210$

Or we can write as follows:

$\$1,100(1+0.10) = \$1,210$

$\$1,000(1+0.10)(1+0.10) = \$1,210$

$\$1,000(1+0.10)^2 = \$1,210$

Now, if you invest $1,210 for the third year at 10%, the value of your investment would be

$\$1,210(1+0.10) = \$1,331$

We can also write the above equation as

$\$1,000(1+0.10)(1+0.10)(1+0.10) = \$1,331$

⇒

$\$1,000(1+0.10)^3 = \$1,331$

We can continue this way for years 4 and 5 with outcomes as follows:

$\$1,000(1+0.10)^4 = \$1,464.10$

$\$1,000(1+0.10)^5 = \$1,610.51$

In this case, your investment of $1,000 earns $610.51 at the end of five years. The value of your investment grows to $1,610.51 rather than $1,500.

In the above example, (1+0.10), (1+0.10)², (1+0.10)³, (1+0.10)⁴, (1+0.10)⁵ show how $1 investment grows every year:

$(1+0.10) = 1.10$

$(1+0.10)^2= 1.21$

$(1+0.10)^3= 1.331$

$(1+0.10)^4= 1.4641$

$(1+0.10)^5= 1.61051$

If you subtract $1 in each equation above, we get the effective interest rate:

$(1+0.10) - 1= 0.10$

$(1+0.10)^2 - 1 = 0.21$

$(1+0.10)^3 - 1 = 0.331$

$(1+0.10)^4 - 1 = 0.4641$

$(1+0.10)^5 -1 = 0.61051$

The effective interest rate when the interest rate compounds annually,

$\left(1+r\right)^t - 1$

Compare the above calculations with the simple interest rate, where interest rates do not compound. It remains 10% without compounding annually. When 10% compounds annually, the effective rate increases from 10% in the first year to 61.051% in the fifth year.

As you can see now that a $1,000 investment at a 10% continuously compounded interest rate can $610.51 as opposed to $500 with a simple interest rate.

Let's $$1,000 = M₀, and (1+0.10)^t = (1+r)^t, then we can write, Future Value, FV_t:

$M_t = M_0(1+r)^t$

In other words, the future value of $1 can be written as (1+r)^t, which is the compound factor.

Let's now consider one year:

When we compound r semi-annually in one year the amount $1 grows to
$\left(1+\frac{r}{2}\right)^2$
When we compound r quarterly in one year the amount $1 grows to
$\left(1+\frac{r}{4}\right)^4$
When we compound r monthly in one year the amount $1 grows to
$\left(1+\frac{r}{12}\right)^{12}$
When we compound r weekly in one year the amount $1 grows to
$\left(1+\frac{r}{52}\right)^{52}$
When we compound r daily in one year the amount $1 grows to
$\left(1+\frac{r}{365}\right)^{365}$

Thus, in general, when we compound r m-times in one year the amount $1 grows to

$\left(1+\frac{r}{m}\right)^m$

Let's now consider t years:

When we compound r m-times in one year for t years the amount $1 grows to

$\left(1+\frac{r}{m}\right)^{mt}$

Therefore, Future value:

$M_t = M_0 \left(1+\frac{r}{m} \right)^{mt}$

Let's consider the following example:

✓ Example 2

(a) You are given: t = 3, m = 2, r = 8%, M₀ = $5000, what is future value, M₃?

(b) You are given: t = 3, m = 12, r = 8%, P₀ = $5000, what is future value, M₁₂?

Solution:

(a)

$M_t = M_0 \left(1+\frac{r}{m}\right)^{mt}$

$M_2 = 5,000 \left(1+\frac{0.08}{2} \right)^{2\times 3} = 5,000(1+0.04)^6=5000(1.265) = 6,325$

(b)

$M_t = M_0 \left(1+\frac{r}{m} \right)^{mt}$

$M_12 = 5,000 \left(1+\frac{0.08}{12} \right)^{12\times 3} = 5,000\left(1+0.0067\right)^{36}=5000\left(1.272\right)=6,360$

Continuously Compounding Interest Rate

Posted on 20222022 by M. Humayun Kabir

Continuous Compounding

In the limit, we compound increasingly frequently to obtain continuously compounded interest rates. In our previous formulation,

(1) $\begin{equation*} \left(1+\frac{r}{m} \right)^m\end{equation*}$

if we increase m to infinity, then we can express it as

(2) $\begin{equation*} \lim_{m\to \infty}\left(1+\frac{r}{m} \right)^m = e^r\end{equation*}$

e^r is an exponential function. e is a mathematical constant, the value of approximately 2.71828…. . Yes, it's ....., which means more digits, and it continues forever. However, we use 2.718 or 2.72 as an approximation. e shows up whenever systems grow exponentially and continuously, for example, interest rate. We can write e as follows:

(3) $\begin{equation*} e=\sum_{n=0}^{\infty}{\frac{1}{n!}}={\frac{1}{0!}}+{\frac{1}{1!}}+{\frac{1}{2!}}+{\frac{1}{3!}}+\dots \end{equation*}$

where, n! is the factorial of a positive integer n, and can be expressed as:

(4) $\begin{equation*} n! = 1 \times 2 \times 3 \times ........ \times (n-2) \times (n-1) \times n\end{equation*}$

For example,

(5) $\begin{equation*} 2! = 2 \times 1=2 \end{equation*}$

(6) $\begin{equation*} 3! = 3 \times 2 \times 1=6 \end{equation*}$

(7) $\begin{equation*} 4! = 4 \times 3 \times 2 \times 1=24 \end{equation*}$

Remember,

(8) $\begin{equation*} 0! = 1 \end{equation*}$

is called empty product. So, we can write,

(9) $\begin{equation*} e=\sum_{n=0}^{\infty}{\frac{1}{n!}}={\frac{1}{1}}+{\frac{1}{1\times 1}}+{\frac{1}{1\times 2}}+{\frac{1}{1\times 2\times 3}}+\dots \end{equation*}$

(10) $\begin{equation*} e=1+\left(1+{\frac{1}{2}}+{\frac{1}{6}}+\dots\right) \end{equation*}$

Let's try to explain the above equation with an example. Imagine, you deposit $1 in the bank with an interest rate of 100% per unit of time. This 'per unit' can be 1 year or 1 month, 1 hour. Here 1 is the unit of measurement. The first 1 outside the bracket in the equation is your $1 deposit or principal. The first 1 in the bracket is the interest earned on the principal as the interest rate is 100%.

Now divide the whole time into two equal lengths. Each length would be 1/2. Then the interest earned on the previous interest of $1 dollar would be 1/2 or $0.5, which is the second element in the bracket. In other words, it is the interest on interest.

Now divide the whole time into three equal lengths, each length would be 1/3. Then the interest earned on the previous interest of $1 dollar and the following interest of 1/2 would be

(11) $\begin{equation*} \frac{1}{6} \left(={\frac{1}{2}}\times{\frac{1}{3}}\right) \end{equation*}$

which is third element in the bracket.

This way it continues forever. As a result,

(12) $\begin{equation*} \left(1+{\frac{1}{2}}+{\frac{1}{6}}+\dots\right) \end{equation*}$

represents (interest + interest on interests + interest on interests on interests + ......). Thus, we find the outcome both exponential and continuous. And we say interest rate, r is continuously compounded per unit of time.

(13) $\begin{equation*} \left (1+{\frac{1}{2}}+{\frac{1}{6}}+\dots)\right \end{equation*}$

can be expressed as

(14) $\begin{equation*} \left({\frac{1}{n})\right)^n \end{equation*}$

e is then the limit of

(15) $\begin{equation*} \left (1+{\frac{1}{n}})\right)^n \end{equation*}$

as n approaches infinity. In other words,

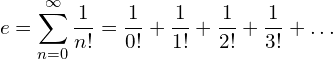
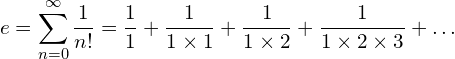
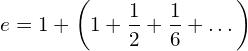
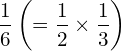
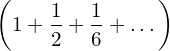
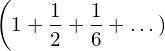
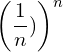
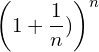
(16) $\begin{equation*} e= \lim_{n\to \infty}\left [1+{\frac{1}{n}\right]}^n \end{equation*}$

Let's r is the interest rate. Then the above equation can be written as

(17) $\begin{equation*} e^r=\sum_{n=0}^{\infty}{\frac{r^n}{n!}}={\frac{1}{0!}}+{\frac{r}{1!}}+{\frac{r^2}{2!}}+{\frac{r^3}{3!}}+\dots= \lim_{n\to \infty}\left [1+{\frac{r}{n}\right]}^n \end{equation*}$

When r = 100% per unit of time, which is continuously compounded, or in decimal format, r = 1, e^r becomes e¹= e, and we end up with equation (5).

What would be the value of $1 if the interest rate, r = 0?

If the interest rate is zero, the principal of $1 will remain $1. This is evident as e^r= e⁰=1.

When r = 25% per unit of time, or in decimal format, r = 0.25, e^r becomes e^0.25, and we end up with:

(18) $\begin{equation*} \lim_{n\to \infty}\left [1+{\frac{0.25}{n}\right]}^n \end{equation*}$

Since the interest rate is normally expressed on a per year basis, and when the rate is also continuously compounded, the above example with a 25% interest rate represents equation (6).

If we continue with 100% interest rate (in decimal, 1) per annum, your $1 becomes

(19) $\begin{equation*} \left(1+r\right) = \left(1+{\frac{1}{1}\right)^1=\$2 \end{equation*}$

with annual compounding (n = 1).

If the bank pays you interest twice a year, then we can say interest rate is compounded semi-annually (n = 2). In other words, the bank is going to pay 50% half-yearly. In such case, your $1 in your account yields

(20) $\begin{equation*} \left(1+{\frac{r}{2}\right)^2 = \left(1+{\frac{1}{2}\right)^2= \$2.25 \end{equation*}$

at the end of the year. Compounding interest rate quarterly (n = 4) yields

(21) $\begin{equation*} \left(1+{\frac{1}{4}\right)^4= \$2.44 \end{equation*}$

and compounding interest rate weekly (n = 52) yields

(22) $\begin{equation*} \left(1+{\frac{1}{52}\right)^{52}= \$2.69 \end{equation*}$

Similarly, compounding daily (n = 365) yields

(23) $\begin{equation*} \left(1+{\frac{1}{365}\right)^{365}= \$2.7145 \end{equation*}$

and compounding daily yields

(24) $\begin{equation*} \left(1+{\frac{1}{365}\right)^{365}= \$2.7145 \end{equation*}$

As the frequency of compounding increases, n grows larger and larger leading to shorter and shorter compounding intervals. Thus, in the limit as n →∞, we get e = 2.71828....

What would be value of $1 in 2 years if the annual interest rate is r with continuously compounding?

It would be

(25) $\begin{equation*} e^{r.2}=\lim_{n\to \infty}\left [1+{\frac{r}{n}\right]}^{n.2} \end{equation*}$

In general, we can write this as:

(26) $\begin{equation*} e^{rt}=\lim_{n\to \infty}\left [1+{\frac{r}{n}\right]}^{nt} \end{equation*}$

Thus, e^rt is what $1 yields in t years with the continuously compounded interest r per annum, where r is expressed in decimal.

Using the first four terms, we get:

(27) $\begin{equation*} e = 1+\left (1+\dfrac{1}{2}+\dfrac{1}{6} \right) = 2.6667 \end{equation*}$

Using the first six terms, we get:

(28) $\begin{equation*} e = 1+\left(1+\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{24}+\dfrac{1}{120} \right)= 2.71667 \end{equation*}$

Similarly, using the first ten terms, we get e = 2.71828. As you can see e converses close to 2.718. Considering t years, we can express it as

(29) $\begin{equation*} \lim_{m\to \infty} \left(1+\frac{r}{m})\right)^{mt} = e^{rt} \end{equation*}$

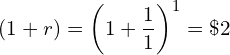
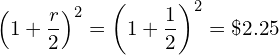
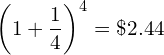
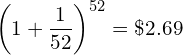
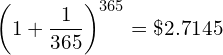
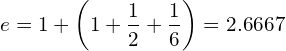
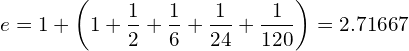
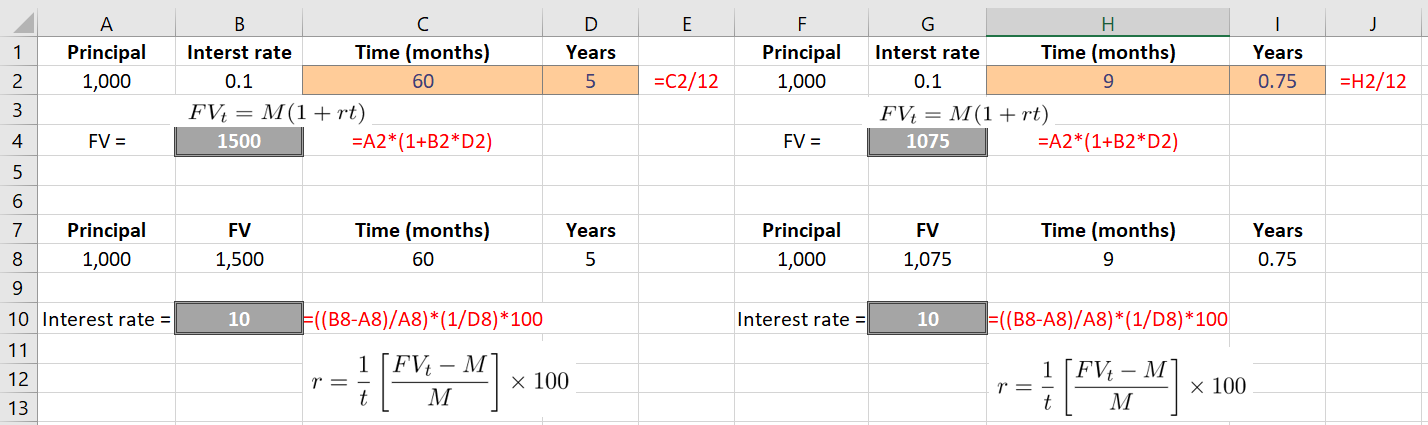
Simple Interest Rate

Posted on 2022 by M. Humayun Kabir

Risk and returns are the most fundamental concepts in business and finance. Any investor who wants to earn a return from his/her investment must face the risk. The risk is the possibility of losing money when markets move unfavorably. If investors take higher risks in investment, he/she must be compensated for the level of risk through higher expected returns. Before we dig further into such a relation, we must understand interest rate compounding and how the returns are calculated.

Simple Interest Rate

If $1,000 is invested for a year at the interest rate of 10% per annum, you are going to receive at the end of the year a return of

$\$1,000 \times 0.10 = \$100$

In this case, your investment earns $100 in a year. Your principal is $1,000. The value of your investment at the end of the first year is $1,100.

If $1,000 is invested for two years at the interest rate of 10% per annum, you are going to receive at the end of the first year a return of

$\$1,000 \times 0.10 = \$100$

The future value of your investment in one year is

$FV_1 = \$1,000 + \$1,000 \times 0.10 \times 1 = \$1,000(1 + \times 0.10 \times 1) = \$1,100$

At the end of the second year, you are going to receive a return of

$\$1,000 \times 0.10 = \$100$

In this case, your investment earns $100 in the first year and another $100 in the second year. In two years your $1,000 investment results in $100 + $100 = $200 returns. The value of your investment in two years is $1,200. We can also write this as

The future value of your investment in two years is

$FV_2 = \$1,000 + \$1,000 \times 0.10 \times 2 = \$1,000(1 + 0.10 \times 2) = \$1,200$

If you continue the process for three, four, and five years, each year you continue to earn $100. In five years, your $1,000 would earn $500.

The future value of your investment in five years is

$FV_5 = \$1,000 + \$1,000 \times 0.10 \times 5 = \$1,000(1 + 0.10 \times 5) = \$1,500$

The following table shows the interest rate calculations for five years:

Rendered by QuickLaTeX.com
Let's $1,000 = M, and 10% = i, then we can write:

The value of the investment in t year

$FV_t= M(1+rt)$

If you are given the initial value of an investment, M, maturity of your investment, t, and the future value of the investment, FV_t, then the rate of interest can be derived as

$FV_t= M(1+rt)$

$1+rt = {\frac{FV_t}{M}$

$rt = {\frac{FV_t}{M} - 1$

$r = \frac{1}{t}\left [\frac{FV_t}{M} - 1\right]$

$r = \frac{1}{t}\left [\frac{FV_t-M}{M}\right]$

In percentage, we can write,

$r = \frac{1}{t}\left [\frac{FV_t-M}{M}\right]\times 100$

where, FV_t- M is the total interest earned over t-periods, and M is the principal. Then the interest earned per dollar investment is:

$\frac{FV_t-M}{M}$

Since FV_t - M = total interest earned, we can also write the above formula as

$r = \frac{\text {Total interest}}{M \times t} \times 100$

Remember, t is always expressed in years. If you invest for 9 months, t would be 6/12 = 0.5.

In Excel, we can calculate FV and simple interest rates. Follow the examples in Excel below.

You can do similarly in Python.

Tip: Click the arrow on the right side of the cell to evaluate (arrow is shown on mouseover). OR press Shift-ENTER

In the above example, every year, you earn 10% on your principal. The interest that you earn in the first year is not re-invested. It is as if you are withdrawing $100 that you earn as interest income and keep investing the same $1,000 repeatedly. This way, you are missing the interest income that you could earn on the interest income every year. If you could do so, how that would look like? Let's see.