Continuous Compounding
In the limit, we compound increasingly frequently to obtain continuously compounded interest rates. In our previous formulation,
(1) ![]()
if we increase m to infinity, then we can express it as
(2) ![]()
er is an exponential function. e is a mathematical constant, the value of approximately 2.71828…. . Yes, it's ....., which means more digits, and it continues forever. However, we use 2.718 or 2.72 as an approximation. e shows up whenever systems grow exponentially and continuously, for example, interest rate. We can write e as follows:
(3) 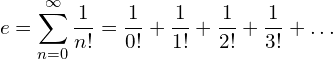
where, n! is the factorial of a positive integer n, and can be expressed as:
(4) ![]()
For example,
(5) ![]()
(6) ![]()
(7) ![]()
Remember,
(8) ![]()
(9) 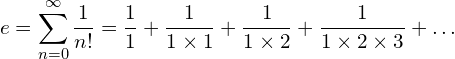
(10) 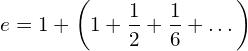
Let's try to explain the above equation with an example. Imagine, you deposit $1 in the bank with an interest rate of 100% per unit of time. This 'per unit' can be 1 year or 1 month, 1 hour. Here 1 is the unit of measurement. The first 1 outside the bracket in the equation is your $1 deposit or principal. The first 1 in the bracket is the interest earned on the principal as the interest rate is 100%.
Now divide the whole time into two equal lengths. Each length would be 1/2. Then the interest earned on the previous interest of $1 dollar would be 1/2 or $0.5, which is the second element in the bracket. In other words, it is the interest on interest.
Now divide the whole time into three equal lengths, each length would be 1/3. Then the interest earned on the previous interest of $1 dollar and the following interest of 1/2 would be
(11) 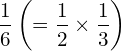
which is third element in the bracket.
This way it continues forever. As a result,
(12) 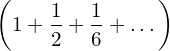
represents (interest + interest on interests + interest on interests on interests + ......). Thus, we find the outcome both exponential and continuous. And we say interest rate, r is continuously compounded per unit of time.
(13) 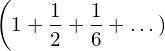
(14) 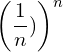
e is then the limit of
(15) 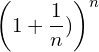
as n approaches infinity. In other words,
(16) ![Rendered by QuickLaTeX.com \begin{equation*} e= \lim_{n\to \infty}\left [1+{\frac{1}{n}\right]}^n \end{equation*}](https://myriskbook.com/wp-content/ql-cache/quicklatex.com-c7b276c7dd6c6790ccd3c0095c772f04_l3.png)
Let's r is the interest rate. Then the above equation can be written as
(17) ![Rendered by QuickLaTeX.com \begin{equation*} e^r=\sum_{n=0}^{\infty}{\frac{r^n}{n!}}={\frac{1}{0!}}+{\frac{r}{1!}}+{\frac{r^2}{2!}}+{\frac{r^3}{3!}}+\dots= \lim_{n\to \infty}\left [1+{\frac{r}{n}\right]}^n \end{equation*}](https://myriskbook.com/wp-content/ql-cache/quicklatex.com-29751f9dcd22e4474101e3870800dc22_l3.png)
When r = 100% per unit of time, which is continuously compounded, or in decimal format, r = 1, er becomes e1 = e, and we end up with equation (5).
What would be the value of $1 if the interest rate, r = 0?
If the interest rate is zero, the principal of $1 will remain $1. This is evident as er = e0 =1.
When r = 25% per unit of time, or in decimal format, r = 0.25, er becomes e0.25, and we end up with:
(18) ![Rendered by QuickLaTeX.com \begin{equation*} \lim_{n\to \infty}\left [1+{\frac{0.25}{n}\right]}^n \end{equation*}](https://myriskbook.com/wp-content/ql-cache/quicklatex.com-aeeca399abdc2acd6fe8dcf0e6e84b0f_l3.png)
Since the interest rate is normally expressed on a per year basis, and when the rate is also continuously compounded, the above example with a 25% interest rate represents equation (6).
If we continue with 100% interest rate (in decimal, 1) per annum, your $1 becomes
(19) 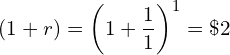
with annual compounding (n = 1).
If the bank pays you interest twice a year, then we can say interest rate is compounded semi-annually (n = 2). In other words, the bank is going to pay 50% half-yearly. In such case, your $1 in your account yields
(20) 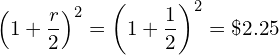
at the end of the year. Compounding interest rate quarterly (n = 4) yields
(21) 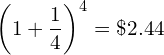
and compounding interest rate weekly (n = 52) yields
(22) 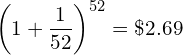
Similarly, compounding daily (n = 365) yields
(23) 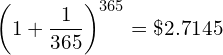
and compounding daily yields
(24) 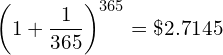
As the frequency of compounding increases, n grows larger and larger leading to shorter and shorter compounding intervals. Thus, in the limit as n →∞, we get e = 2.71828....
What would be value of $1 in 2 years if the annual interest rate is r with continuously compounding?
It would be
(25) ![]()
In general, we can write this as:
(26) ![]()
Thus, ert is what $1 yields in t years with the continuously compounded interest r per annum, where r is expressed in decimal.
Using the first four terms, we get:
(27) 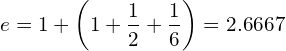
Using the first six terms, we get:
(28) 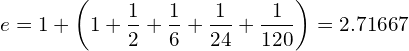
Similarly, using the first ten terms, we get e = 2.71828. As you can see e converses close to 2.718. Considering t years, we can express it as
(29) ![]()