Simple Interest Rate - My Risk Book

Risk and returns are the most fundamental concepts in business and finance. Any investor who wants to earn a return from his/her investment must face the risk. The risk is the possibility of losing money when markets move unfavorably. If investors take higher risks in investment, he/she must be compensated for the level of risk through higher expected returns. Before we dig further into such a relation, we must understand interest rate compounding and how the returns are calculated.

Simple Interest Rate

If $1,000 is invested for a year at the interest rate of 10% per annum, you are going to receive at the end of the year a return of

$\$1,000 \times 0.10 = \$100$

In this case, your investment earns $100 in a year. Your principal is $1,000. The value of your investment at the end of the first year is $1,100.

If $1,000 is invested for two years at the interest rate of 10% per annum, you are going to receive at the end of the first year a return of

$\$1,000 \times 0.10 = \$100$

The future value of your investment in one year is

$FV_1 = \$1,000 + \$1,000 \times 0.10 \times 1 = \$1,000(1 + \times 0.10 \times 1) = \$1,100$

At the end of the second year, you are going to receive a return of

$\$1,000 \times 0.10 = \$100$

In this case, your investment earns $100 in the first year and another $100 in the second year. In two years your $1,000 investment results in $100 + $100 = $200 returns. The value of your investment in two years is $1,200. We can also write this as

The future value of your investment in two years is

$FV_2 = \$1,000 + \$1,000 \times 0.10 \times 2 = \$1,000(1 + 0.10 \times 2) = \$1,200$

If you continue the process for three, four, and five years, each year you continue to earn $100. In five years, your $1,000 would earn $500.

The future value of your investment in five years is

$FV_5 = \$1,000 + \$1,000 \times 0.10 \times 5 = \$1,000(1 + 0.10 \times 5) = \$1,500$

The following table shows the interest rate calculations for five years:

Rendered by QuickLaTeX.com
Let's $1,000 = M, and 10% = i, then we can write:

The value of the investment in t year

$FV_t= M(1+rt)$

If you are given the initial value of an investment, M, maturity of your investment, t, and the future value of the investment, FV_t, then the rate of interest can be derived as

$FV_t= M(1+rt)$

$1+rt = {\frac{FV_t}{M}$

$rt = {\frac{FV_t}{M} - 1$

$r = \frac{1}{t}\left [\frac{FV_t}{M} - 1\right]$

$r = \frac{1}{t}\left [\frac{FV_t-M}{M}\right]$

In percentage, we can write,

$r = \frac{1}{t}\left [\frac{FV_t-M}{M}\right]\times 100$

where, FV_t- M is the total interest earned over t-periods, and M is the principal. Then the interest earned per dollar investment is:

$\frac{FV_t-M}{M}$

Since FV_t - M = total interest earned, we can also write the above formula as

$r = \frac{\text {Total interest}}{M \times t} \times 100$

Remember, t is always expressed in years. If you invest for 9 months, t would be 6/12 = 0.5.

In Excel, we can calculate FV and simple interest rates. Follow the examples in Excel below.

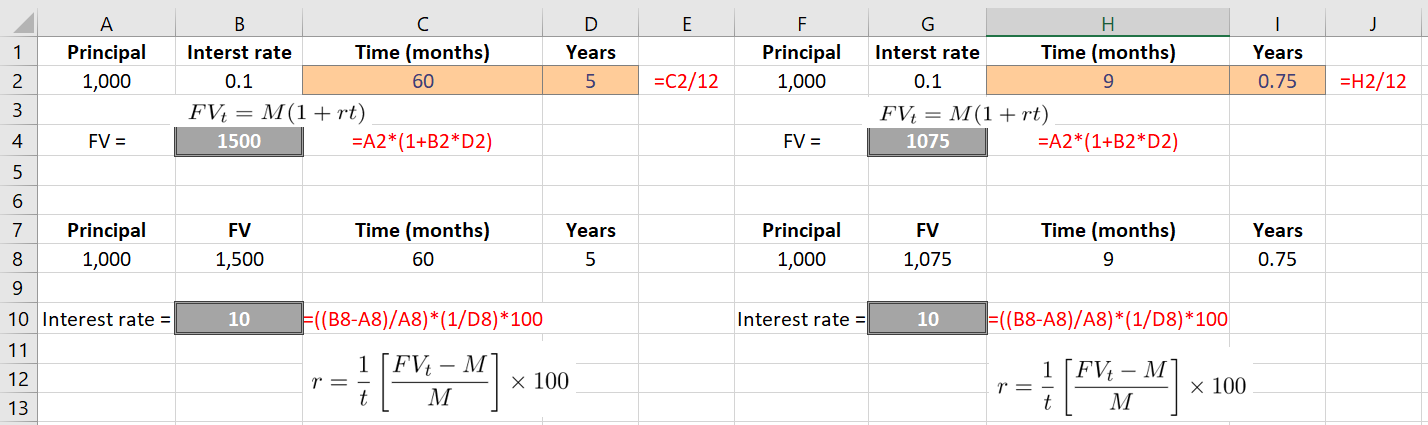
You can do similarly in Python.

Tip: Click the arrow on the right side of the cell to evaluate (arrow is shown on mouseover). OR press Shift-ENTER

In the above example, every year, you earn 10% on your principal. The interest that you earn in the first year is not re-invested. It is as if you are withdrawing $100 that you earn as interest income and keep investing the same $1,000 repeatedly. This way, you are missing the interest income that you could earn on the interest income every year. If you could do so, how that would look like? Let's see.